1)Անհավասարումը լուծե՛ք միջակայքերի եղանակով.
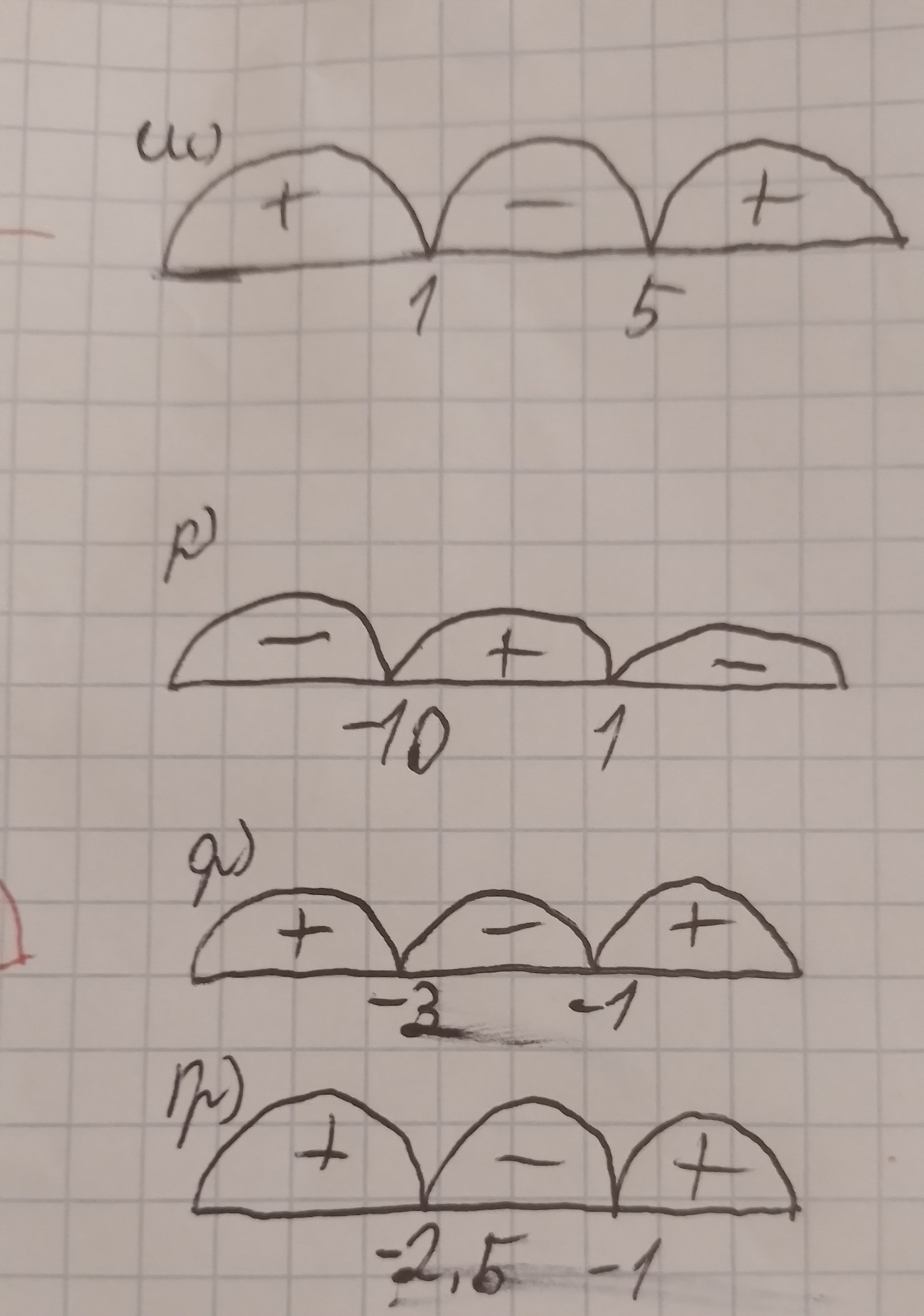
ա) x² — 6x + 5 > 0

36-20=16

x1=6+4/2=5

x2=6-4/2=1

(-;1)U(5;+)

բ) — x² + 9x + 10 >= 0

81+40=121

x1=-9-11/2=-10

x2=-9+11/2=1

-(x+10)(x-1)>=0

(-10;1)

գ) 3x² + 12x + 9 <= 0

144-108=36

x2=-12+6/6=-1

x1=-12-6/6=-3

3(x+3)(x+1)>=0

(-;-3)U(-1;+)

դ) 4x² + 14x +10 > 0

196-160=√36=6

x1=-14-6/8=-20=-2.5

x2=-14+6/8=-1

4(x+2.5)(x+1)

(-;-2.5)U(-1;+)

2)Անհավասարումը լուծե՛ք գրաֆիկական եղանակով.
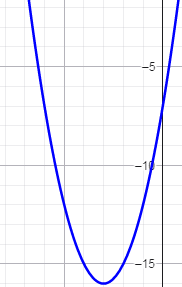
ա) x² + 6x — 7 > 0

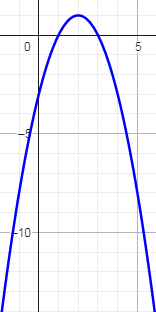
բ) — x² + 4x — 3 <= 0

գ) — 4x² — 6x + 5 >= 7

 

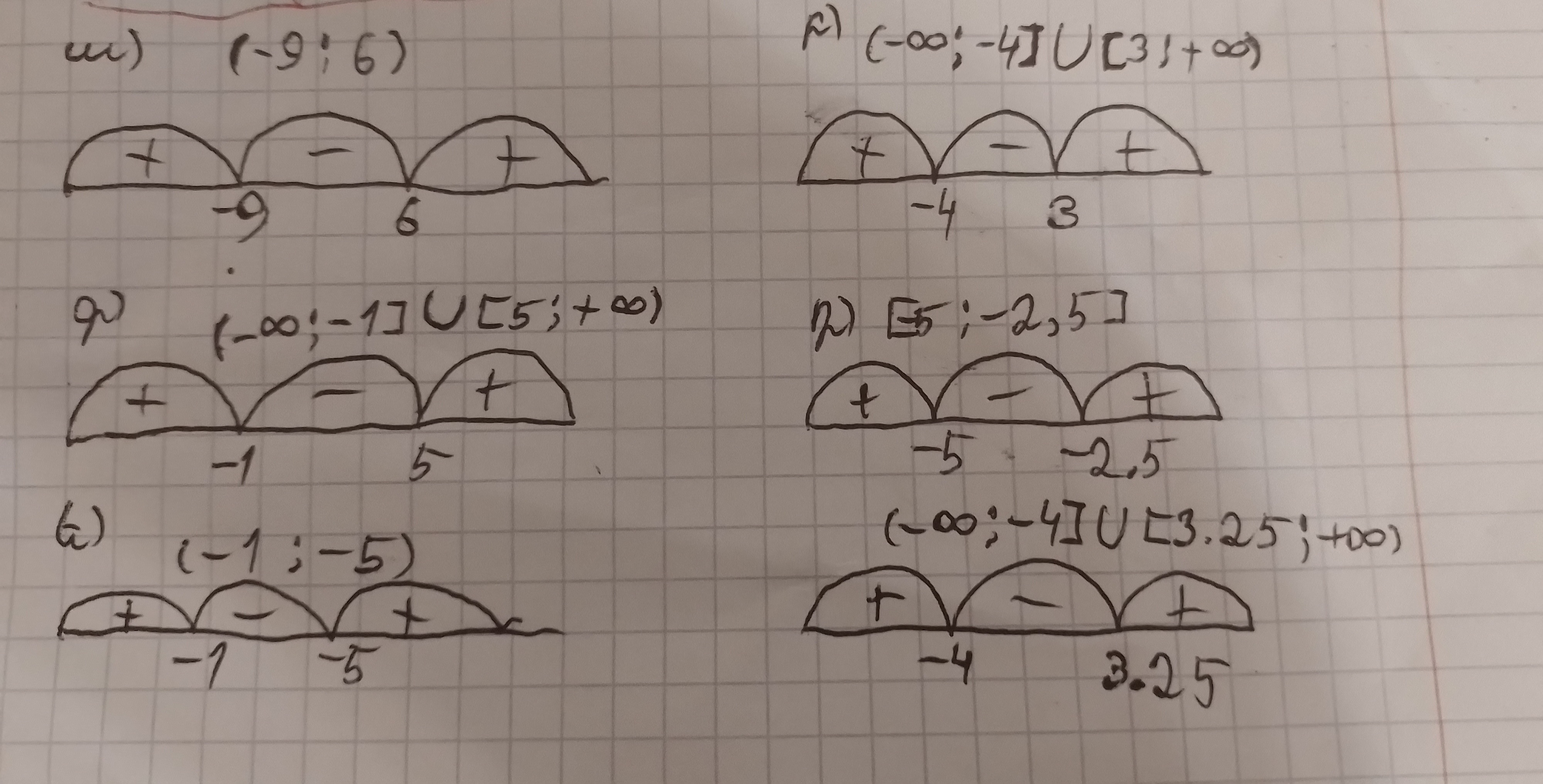
3)Լուծե՛ք անհավասարումը.

ա) (x — 6)(x + 9) < 0

բ) (x + 4)(x — 3) >= 0

գ) (x — 5)(x + 1) >= 0

դ) (2x + 5)(x + 5) <= 0

ե) — 3(x + 1)(x — 5) > 0

զ) — 2(x + 4)(x — 3.25) <= 0